RS纠删码

在存储系统中，需要采用数据冗余技术来保证数据的可靠性，相比使用多副本复制机制外，使用纠删码能够以更小的数据冗余度获得更高的数据可靠性。Reed Solomon Coding是存储领域常用的一种纠删码。

RS纠删码将原始文件分成n个数据块，同时为这n个数据块生成m个校验块，而能够容忍最多丢失（只保证丢失而不保证数据篡改）这（n+m)个块中的任意m个数据或者校验块。

RS编码以word为单位进行编码和解码（word字长一般为8或者16），而大的数据块拆分成一个个word进行编解码。

假如有数据块内容为ABCDEFGHIJKLMNOP，将其分为四个数据块，每个数据块包含四个word（字长为8），我们使用矩阵来表示这四个数据块，对应的数据矩阵如下：

接着使用编码矩阵来对数据矩阵进行编码，产生数据块和校验块：

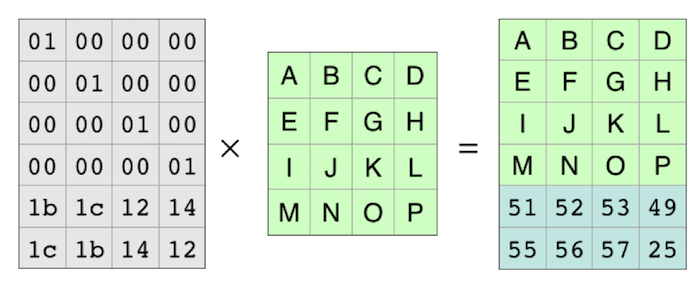
上图左边的矩阵为编码矩阵，该矩阵由上面一个4X4的单位矩阵和下面一个2X4的Vandermonder矩阵组成。这里的2对应上面的m，表明需要生成2个校验块，4是因为原数据分成了4个数据块。我们可以看到右边经过编码矩阵处理后的结果，比原来的数据矩阵多了两行，即对应两个校验块。

因为m取的是2，因此最多允许丢失2个块，这里我们假设IJKL和MNOP两个块被丢失了：

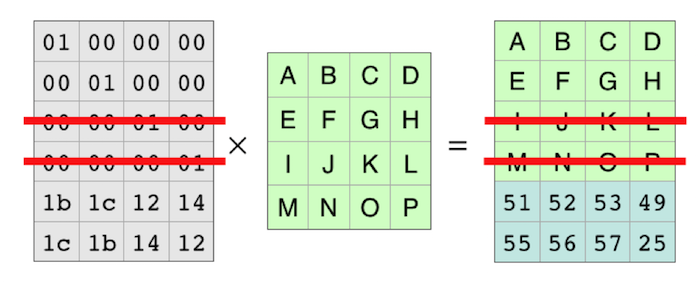
我们在编码矩阵和结果矩阵将对应的第3，4行删除，等式两边仍然成立：

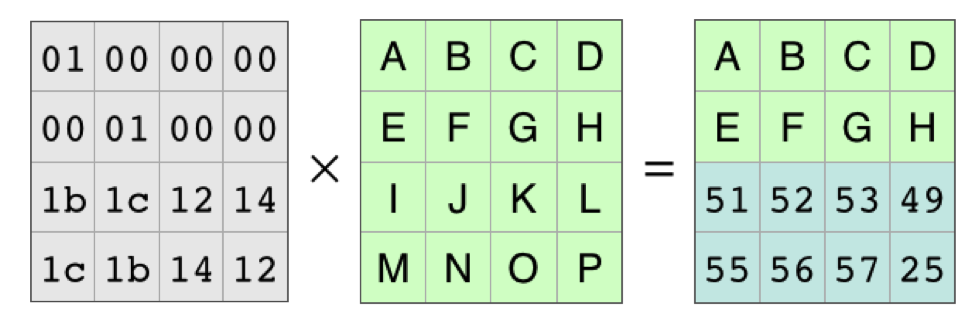
现在的编码矩阵是原来的一部分，我们将其记为C1，接着我们分别在两边乘以编码矩阵的逆矩阵：

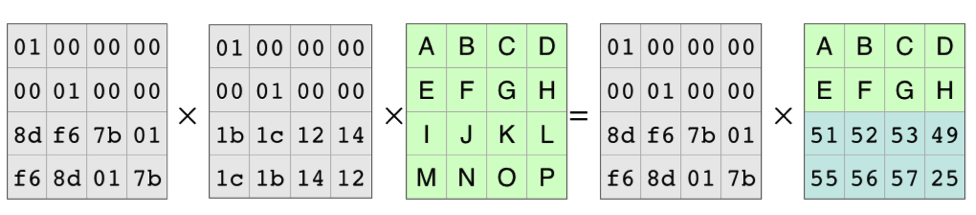
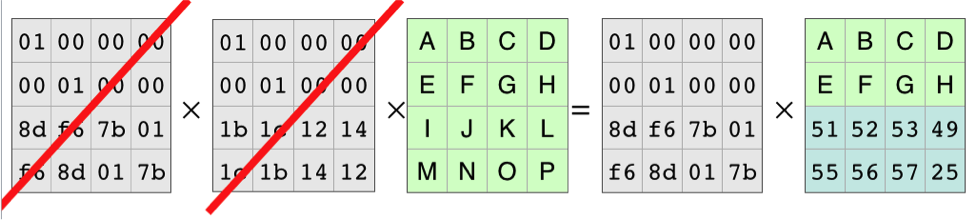
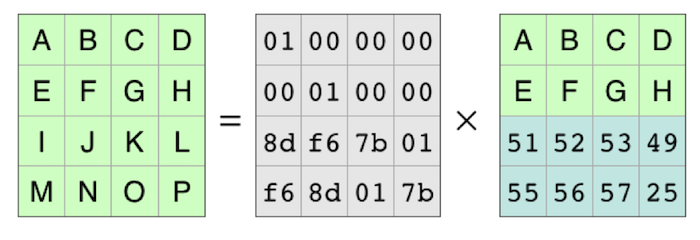
我们可以看到，我们可以从编码产生的6个块中的任意4个块中恢复原数据。

在上面中，为了恢复原数据，需要计算编码矩阵（这里指的是C1）的逆矩阵，这也是为什么上面编码矩阵是由一个单位矩阵和一个Vandermonder矩阵组成的，因为Vandermonder矩阵任意两行之间都线性无关，可以求解出逆矩阵。

RS纠删码是按照word为单位对数据进行编解码，这也就要求对一个字进行编码后，产生的结果仍然是一个字，因此RS纠删码基于伽罗华域GF(2^n)及其四则运算来进行编解码。

这里使用GF(2^4)，并且取n和m都为3来举个例子。

首先，GF(2^4)共有0~15这16个元素，首先构造exp表和log表：

i	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
log	-	0	1	4	2	8	5	10	3	14	9	7	6	13	11	12
exp	1	2	4	8	3	6	12	11	5	10	7	14	15	13	9	1

假设原始数据 D, Vandermonde 矩阵 F, 冗余数据 C，则：

上面计算矩阵F时，根据GF(2^4)的计算规则，3^2^ = 3*3 = exp(log(3)+log(3)) = 5

将矩阵F与3*3的单位矩阵E集合，可得：

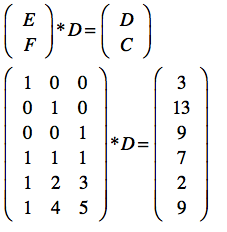
根据上面的定义，任意丢失3份数据，都可以恢复原来的数据，这里假设丢失了D2，D3和C3，则恢复过程：

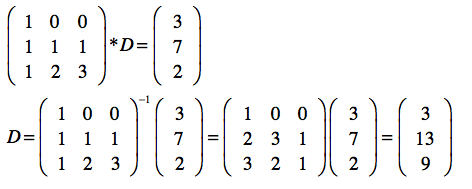
可以看到，成功恢复原来的数据。