红黑树是特殊的4阶b-tree,也就是2-3-4 tree。
根据 Knuth 的定义,一个 m 阶的B树是一个有以下属性的树:
- 每一个节点最多有 m 个子节点
- 每一个非叶子节点(除根节点)最少有 ⌈m/2⌉ 个(向上取整)子节点,比如5阶B树则最少要有3个子节点
- 如果根节点不是叶子节点,那么它至少有两个子节点
- 有 k 个子节点的非叶子节点拥有 k − 1 个键
- 所有的叶子节点都在同一层
b-tree插入新的节点时,如果当前节点满了,也就是上溢,则分裂成一个父键和两个子节点,将父键插入到原节点的父节点中;插入之后,如果原节点的父节点也上溢了,则继续分裂,插入
b-tree删除节点时,首先转换成删除前驱节点或者后继节点;如果导致当前键数量不足 ⌈m/2⌉-1,也就是下溢,则首先尝试向sibling借一个键;如果sibling不足以借出,则sibling的键个数刚好处于 ⌈m/2⌉-1,这时候这将两个子结点和父节点的一个键进行合并,这时候新的节点键个数刚好为m-1个。由于合并时需要一个父节点的键,相当于从父节点删除了这个键,如果导致父节点发生下溢,则同样,首先尝试从父节点的sibling借一个键,如果sibling不足以借出,则合并
红黑树的性质
红黑树是二叉搜索树,除了具备二叉搜索树的性质之外,还具有下列性质:
- 节点是
BLACK或者RED - 根节点总是
BLACK RED节点的子结点只能是BLACK节点,不能有两个RED节点相连- 叶子节点总是空的
BLACK节点;从根节点到叶子节点的所有路径,具有相同数量的BLACK节点。因此rb-tree树中的最长路径最长只会是最短路径的两倍。其中最长路径为黑红交替,最短路径为全黑。该性质确保红黑树不会退化成链表,保证了搜索效率。
红黑树是从2-3-4树演化过来的,一个黑色节点和一个红色节点组成一个3-node,一个黑色节点和两个红色节点组成一个4-node:

红黑树的黑色节点,可以看成是2-3-4树节点中的中间key。将红黑树与2-3-4树联系起来,就很容易理解红黑树的几个性质了。
查询
二叉搜索树常规操作。
插入
为了不破坏性质4,新插入的节点总是红色的。
如果新插入的节点,其父节点是黑色的,那么这时候不会破坏红黑树的性质,插入完成。
如果新插入的节点,其uncle节点也是红色的:

如上图,这时候,可以看成是往一个4-node 插入了新值,这时候需要将4-node分裂成一个2-node和一个3-node,对应的操作就是将gp设置成RED,将p和uncle设置成BLACK。gp设置成RED,也就是将gp插入其父节点所在的node中,可能会触发新的分裂,这是一个递归的过程。
而当uncle节点是BLACK,说明当前节点还没有满,不需要分裂。有时候需要进行rotate,调整一下BLACK节点的位置:

如果uncle是BLACK,说明uncle是属于其他node,而new,p,和gp组成一个4-node。而这时候p才是4-node的中间,需要对gp执行right-rotate以及重新着色。

这种情况,p,new和gp组成一个4-ndoe,而new才是中间,需要先对p执行left-rotate再对gp执行right-rotate,然后重新着色
可以看到,红黑树的插入,只需执行多次重新着色以及最多两次rotate,是比较高效。
删除
先按照BST的常规做法,使用待删除节点的前驱或者后继节点替代,转变为删除前驱或者后继节点,记为x
如果x是红色的,直接删除,不会破坏红黑树的规则
如果x具有一个红色的child,说明当前节点是
3-node,使用child节点替代并染成黑色,完成删除说明当前节点是一个
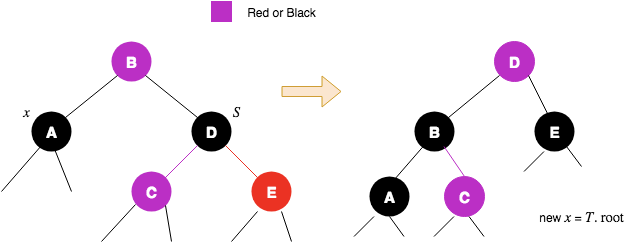
2-node,需要向sibling借或者与parent合并3.1 如果sibling是红色的,说明parent是一个3-node,这时候先对parent执行rotate,将sibling转变为3-node的中间节点,即黑色的,而当前的parent则变成红色,更新x当前新的sibling。B树删除时,会先考虑向slibing借一个节点,但是实际上是向父节点拿一个节点,然后从sibling拿一个节点补充给父节点。我们这一步rotate,是要设置x真正的sibling。
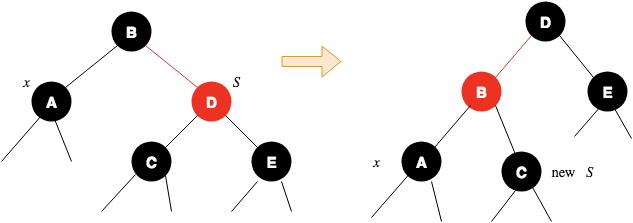
3.2 如果sibling的两个子节点都是黑色的,说明silbing也是一个2-node,这时候无法向sibling借一个节点,因此需要与父节点合并,将sibling变为red;如果parent是红色的,说明x的grantprarent至少是3-node,并不会导致其产生下溢,将其变成黑色的,完成删除。如果x的parent是黑色的,则可以看成当前正在删除x的parent,设置x为x.parent,从3.1重新开始
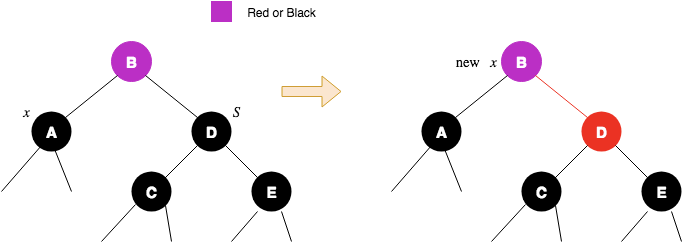
3.3 如果当前节点是左分支,且sibling的左儿子是红色的,右儿子是黑色的,则sibling是一个3-node,可以借出一个节点,但是需要先调换sibling和sibling.left的颜色,然后对sibling进行right rotate,本质上就是原来sibling是3-node的中间key,现在需要调换sibling.left为中间key,继续下一步;如果当前节点是右分支,与之类似
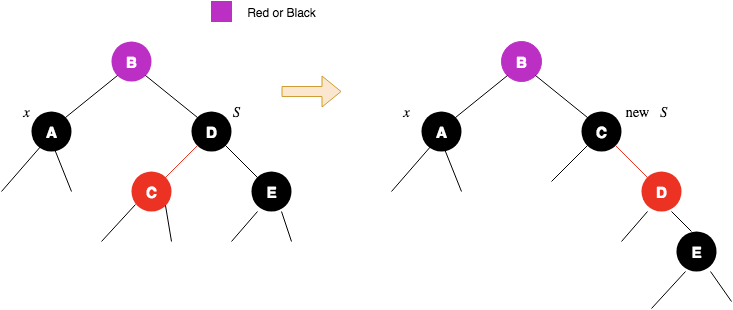
3.4 如果当前节点是左分支,且sibling的右儿子是红色的,那么sibling是一个3-node或者4-node,这时候可以借出节点,将sibling的颜色设置为parent的颜色,sibling的right设置为黑色,parent设置为黑色,然后对parent执行left rotate,完成删除。本质上是借出sibling,然后sibling.right变成中间节点;如果是右分支,与之类似